

| How To Avoid Nearsightedness
|
The formulation of a problem is often far more essential than its solution, which may be a matter of mathematical or experimental skill. To raise new questions, new possibilities, to regard old problems from a new angle, requires creative imagination and marks real advances in science. - Albert Einstein
There has been an immense concentration on the defective eye and correspondingly little interest in establishing the fundamental behavior characteristic of the normal eye.
Dr. Francis Young, over a period of thirty years, has been able to establish the fact that the normal eye tracks its average visual environment with 0.97 as the correlation coefficient. When you make a slight shift in your average visual environment, the normal eye makes a corresponding focal state shift by the same quantitative amount. There are many other indications that, whenever the normal eye is correctly tested, it will always show this fundamental (bi-directional focal control) behavior characteristic.
The analog computer presented in this chapter is a prototype. Later chapters further refine the concept that develops from this type of analysis of the normal eye's behavior.
The eye is known to be a complex of feedback control elements. The subject of nearsightedness suggests the question, "How does the normal eye control its long-term growth?". Work done by Dr. Lawrence Stark (1) and others has shown that short-term focus (accommodation) is by feedback control. The process by which the eye grows and controls its focus is a dynamic (closed loop) system. It is impossible to model the normal eye's long-term focusing ability in terms of a heredity (passive) system.
Let us establish a model for the long-term growth of the eye. Stability is not a problem, and our choice shall be a first order system. The transfer function (developed from electrical and control theory engineering) will accurately represent the eye's controlled growth. (Below) (2)
The input to this function is the average value of accommodation of the eye. The equation is implemented by the operational amplifier. (Figure 1)
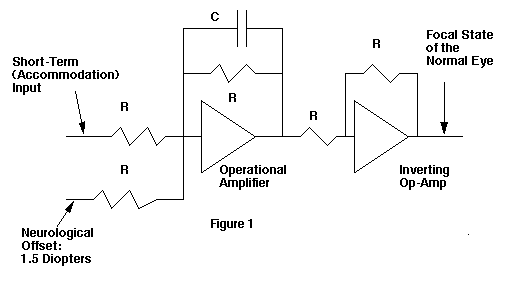
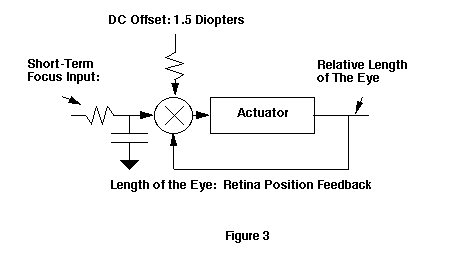
When we build a model we must choose the independent variable and the controlled variable. For the sake of simplicity, we will choose to build a model in which the long-term focal state of the eye is the controlled variable. (Figures 2 and 3)
 |
| The eye's relative focal state is a function of corneal radius and the eye's length. Factual data indicates that these two quantities are under continuous control in the normal eye. |
The author's estimate of the normal eye's time-constant is three months. This parameter is a function of the youthfulness of the individual. (3) Thus, for a child or adolescent, the time-constant is three to four months, while in a young adult, this parameter is more likely to be on the order of five months. (A direct test for the normal eye's time-constant will cause a change of focal state in the normal eye.)
Two additional elements must be included to make our model accurately represent the major facts known about the eye's long-term behavior:
Time scaling is accomplished by the 5,000 micro-farad capacitor and the 10,000 ohm resistor. The time relation chosen is one minute equals one year. Thus, the time-constant of the computer is 20 seconds real time, or four months simulated time.
The offset (DC voltage) applied to the second operational amplifier causes a +1.5 volt offset at the output of the operational amplifier. This represents the +1.5 diopter (average) offset that is observed for the normal primate eye.
This completes the construction of the eye's long-term behavior computer. Space does not permit a more extensive discussion of the computer's development. It is the survivor of many less accurate models. Initially, it was found impossible to model the eye's ordinary growth in terms of a Helmholtz-passive, or heredity model. The prime concern was to keep the model as simple as possible, consistent with the maximum number of facts known about the normal eye's development.
There are several standard methods used to test a normal biological system in order to establish it as a neurological control systems, e.g., impulse, step, and ramp functions. These tests and corresponding responses are well known to electrical and mechanical engineers. The major difficulty in checking a growth system is the length of time taken for results to occur. By computer simulation of the normal eye's behavior, test conditions can be applied and results obtained within minutes, rather than months. This is the major advantages of computer simulation of a physiological process.
By design and necessity, the normal eye is going to function correctly from birth to maturity -- by adjusting its focal state to the average visual environment. We can confirm this basic focal-setting process by changing the average visual environment of the eye. This is shown by the tendency of men, working in the close quarters of missile launch facilities, to develop a negative focal state (myopia) related to their length of service. (4) A step input applied to the computer will produce this same effect. Developing more systematic and quantitative thinking beyond the close work test, we can use a concave lens to artificially create a confined visual environment. In terms of refraction, this lens will move all objects closer to the eye. Applying a negative lens (negative voltage) to our computer produces a change of focal state of the normal eye after several months.
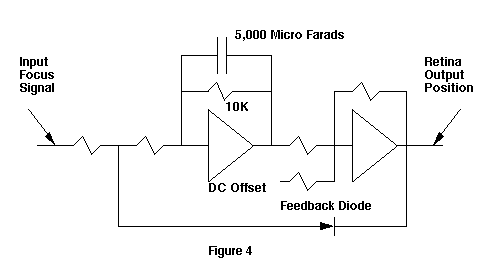 |
| When the normal eye has a negative focal state the image "lifts off" the retina, producing a non-linear control system and a blurred image. The diode in this analog computer simulates the damping effect on the input signal under this condition. This is the major reason that it is so difficult to get the normal eye to move in a positive direction after it has a severe negative focal state. |
The eye can be visualized as a static box camera. In this concept, the front-to-back distance is fixed. If the distance from the cornea to the retina is too great, as a fault of heredity, the eye is nearsighted. This concept simply ignores the necessary dynamic qualities of the normal human eye. The converse of a static camera is a dynamic (cybernetic) model.
From birth to maturity, the eye increases in size by about thirty percent. During this period, the eye's length and cornea shape is continually controlled by the average value of accommodation, thereby maintaining a high level of focal accuracy. The accuracy is estimated to be better than one percent of the total focal power of the normal eye. Only a sophisticated (closed loop) system could cope successfully with such a dynamic process. A study of the literature will substantiate this long-term focal control behavior, not only in animals but in man. (5) (6)
To evaluate two theories, we must consider their predictive capabilities. This requires that the two possible theories yield full quantitative predictions that can be checked against reality by actual test. A decision between the two competing theories can thereby be made. A Helmholtz-heredity theory that yields no qualitative or quantitative predictions and is not consistent with the facts already known about the eye's performance, is nothing more than a sterile tautology.
There are three major requirements of a theory in physical science. They are: (7)
The computer was constructed in compliance with the first two requirements. There is a whole range of predictions to be drawn from the computer. Among the more important are these:
A prediction that can decide between the heredity model and the feedback model is this: It is possible to take any child and intentionally change his focal state by the use of a concave (negative) lens. Clearly, if we can do this, the Helmholtz-heredity theory is not valid as it concerns the fundamental behavior characteristic of the normal eye.
"In the last century, in Russia, minus (concave) glasses were sometimes used to evade military conscription. A few months before the appearance for army examination, the conscript went to an optical doctor and got a pair of strong minus glasses which he wore steadily until prior to the examination. He was then sure that he would be rejected on account of his vision. The minus glasses has changed the focal status of his eyes and made his distant vision very poor." (8)
If anyone doubts this result, the experiment can be repeated. In the model this result is expected. If heredity controls the long-term growth, the above result would not occur. The definitive test between the Helmholtz-passive theory and the Helmholtz-dynamic theory would be to repeat, under controlled conditions, the above uncontrolled test as it pertains to the fundamental behavior characteristic of the normal eye.
1. Stark, L. NEUROLOGICAL CONTROL SYSTEMS, Plenum Press, New York (1966)
2. Milhorn, H. T. THE APPLICATION OF CONTROL THEORY TO PHYSIOLOGICAL SYSTEMS, Chapter 7, Philadelphia, Pa. (1966)
3. Wallman, J. Turkel, J. EXTREME MYOPIA PRODUCED BY MODEST CHANGE IN EARLY VISUAL EXPERIENCE, Science, Vol 201 Sept. (1978)
4. Green, M. A. J. Am Optometry. Assoc. 41 1013 (1970)
5. Young, F. A. "Young tested this close-work theory by keeping pig-tailed macaques seated in a monkey chair in an enclosed visual space for about a year; he reported a change of focal state (adults 0.75 diopter change; young, 1.75 diopter change), which was retained for many months after their removal from the chair." Am. J. Ophthalmology. 53 799 (1961)
6. Rose, L. Yinon, U. Belkin, M. "Cats raised in cages are about 2 diopters negative (myopic) compared with feral (wild) cats." Vision Res. 14, 1029 (1974); Belkin, M. Yinon, U. Rose, L. Reisert, I. DOC Ophthalmology. 42, 433 (1977)
7. Holton, G. Roller, D. FOUNDATIONS OF MODERN PHYSICAL SCIENCE Chapter 8, Redding Massachusetts, Addison-Wesley Publishing Co. (1958)
8. Raphaelson, J. OD Discussions with the author in Cincinnati, Ohio. (1967)