

| How To Avoid Nearsightedness
|
Science consists in grouping facts so that general laws or conclusions may be drawn from them. - Charles Darwin
Our first task is to first define the design equation for the normal eye and to verify the equation by experimental testing. The mathematical model presented in this chapter is a theoretical study of the way in which the normal eye sustains focal accuracy in the presence of focal perturbations and noise.
To obtain clarity of understanding, we have postulated two types of control for the normal eye; genetic and dynamic. To assist our study and understanding we designed, on paper, an automatically focused camera which would have the identical focal control characteristic as the normal eye.
This is, in essence, a black-box technique which we shall use to establish the design equation for the normal eye. We use this approach since we are unable to gain direct access to the device. In choosing our model, we recognize the need for dynamic control to obtain the required accuracy.
The interest of this concept is to develop the ability predict the results of all experimental tests (both theoretical and practical) that we could perform on the normal eye. A further goal is to provide a logical approach for achieving sustained normal vision (a positive focal state) through a technique derived from an accurate understanding of the normal eye.
The problem of the normal eye's negative focal state (myopia) can be seen from two perspectives. The difference between the two theories concerns the way in which the experimental evidence is interpreted. From the traditional perspective, the eye stretches out of shape due to a hereditary defect in the eye's structure. (Thus, the concept that nearsightedness is a defect of the eye.) It is a coincidence that this development occurs while the individual is in a reading (confined) environment. From a dynamic point of view, the normal eye tracks the average value of accommodation and will servo towards, and into, myopia if nothing is done to neutralize the near environment.
The model is presented as the most accurate we can develop. In the previous chapter we have demonstrated very explicit confirmation for this behavioral characteristic of the eye. The model is clear, consistent and accurate with most of the experimental evidence that has been collected. This chapter is indirectly critical of the traditional approach; but only to the extent that it provokes more serious thought about the myopia problem, and the means available to bring about an end to the situation.
Because the normal eye is sophisticated in its design and operational characteristics, the engineering requirement for focal accuracy suggest that the normal eye sets its long-term focus by a dynamic process. The mechanism that maintains the eye's focal status consists of two separate systems. The first system is a blur-driven mechanism that regulates the focal power of the lens for maximum image sharpness. This accommodation system has a time constant of 1/4 second. (1)
The second system, which is responsible for controlling the eye's long-term focus, has a time-constant of 100 days. In a normal visual environment the eye's focal status will be from 0 to +2 diopters. This active system functions to overcome the inevitable perturbations that occur within the eye's optics. (2) The long-term system has a tracking probable error of 1/10 diopters. (3)
Since the focus of a dynamic eye is "slaved" to the average value of accommodation, shifts in the accommodation signal will result in corresponding shifts in the eye's focal status. This predictable consequence of the design has been experimentally verified. (4)
Servo systems are "slave" systems that are defined by their transfer function. We have tentatively established the fact that the normal eye's behavior obeys the following transfer function: (5)
The normal eye's response to a step function is found by:
System's
Response = [ (Step Function) / (s) ] * [ 1 / (TAU s + 1) ]
The eye's time domain response to this step function is: Focus = Offset + Accommodation + Delta * [1 - EXP(- t / TAU ) ]
This equation has been verified by applying a step function to the visual environment of monkeys (previous chapter) and by then measuring the resulting focal status change at two-week intervals for a year.
A servo system will exhibit a response to noise (perturbations) that exists within the control loop. These random focal changes will cause the system to initiate corrective shifts in the eye's focal status. The eye's time domain response to an impulse perturbation is:
Focus = Offset + Accommodation - Perturbation * EXP ( - t / TAU )
These two equations predict the eye's response to two idealized inputs. They do not yield explicit predictions if the eye's visual environment is changing by significant amounts.
We may obtain a piece-wise (iterative) equation for the 1/(TAU s + 1) transfer function by reviewing a block diagram of the eye's focal control system. (See Figure 1)
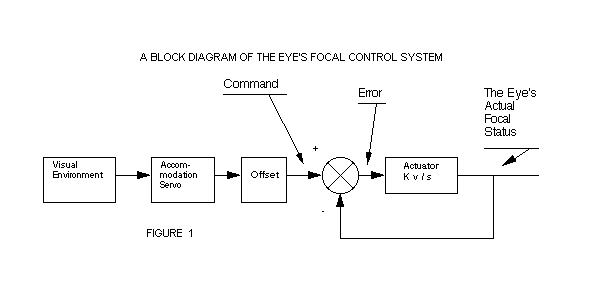
The input for this system is the command signal: (Equation 1)
Commanded Focal Status = Offset + Accommodation (Daily Average)
The error signal is: (Equation 2)
Error
Signal = Commanded Focal Status - The eye's Actual Focal Status
Since the actuator has a very slow velocity constant (K), the amount of error correction achieved in one day is given by: (Equation 3)
Focal Servo Change = Error Signal / TAU
Using this equation, we may calculate the effect of each day's value of accommodation on the eye's focal status: (Equation 4)
Updated
Focal
Status = Yesterday's Focal Status + Focal State Change
Including the effects of random perturbations, the equation becomes; (Combining equations 1, 2, 3 and 4) (Equation 5)
Updated
Focus = [ (Offset + Accommodation-Focus) / TAU ] + Focus - Perturbation
For clarity of analysis in this chapter we will set the perturbation level of the eye to zero diopters. In a normal eye, focal noise and measurement errors produces a measured tracking error of 1/10 diopters. (3)
The equation allows the prediction of the eye's focal status on a continuing basis. Due to the long time-constant of the system, each day's average value of accommodation will have a very small effect on the focal status of the normal eye.
The piece-wise equation provides an alternative method for solving the 1/(TAU s + 1) transfer function. The input for the equation is the signal that is obtained from the accommodation system which is identical to your visual environment.
The piece-wise equation, in this form, predicts the same results that were obtained for a step function change in accommodation (previous chapter) and an impulse perturbation on the eye's focal status.
The hereditary offset is a latent constant of vision. (Figure 2) If a group of individuals have a constant visual environment of -0.5 diopters, their eyes will show a range of focal status values of from zero to two diopters. The mean hereditary offset for the group is +1.5 diopters.
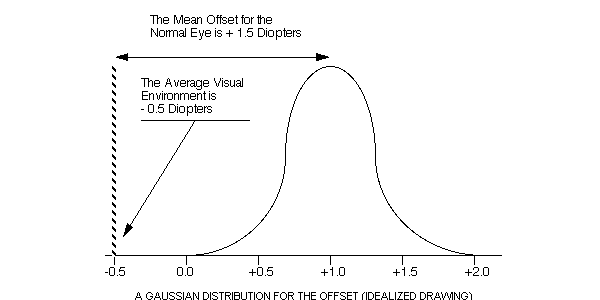
If the average visual environment is changed from -0.5 diopters to -1.5 diopters, the focal status of all individuals will change towards a negative focal state (myopia), as predicted by the equation.
The controlling variable for this equation is the eye's value of accommodation. The focal settings of the lens is determined by information decoded at the surface of the retina. The visual environment may be calculated by the use of the equation:
| VISUAL | |
| ENVIRONMENT = | - 1 / (OBJECT DISTANCE) |
| (In Diopters) | (In Meters) |
A visual object moved inwards from infinity to one meter constitutes an environment change of - 1.0 diopters. Under this circumstance, the accommodation system will servo the lens by + 1.0 diopters to again achieve sharp focus at the surface of the retina.
The average value of accommodation can be determined if an individual's environment is known on a daily basis. If the individual spends eight hours outdoors ( 0 diopters) and eight hours reading (-3.0 diopters) his average visual environment will be -1.5 diopters.
This equation was developed to explain the high level of focal accuracy that is measured in the normal human and primate eye.
We know of few qualitative, and no quantitative theories that can explain focal accuracy of 1/10 diopters for the normal eye. In the absence of any other focal control equation that can provide a logical explanation for such precision, we tentatively propose that this equation and model accurately represents the normal eye's behavior.
Many theories have been developed to explain myopia (as a defect of the eye). Most of these theories suggest a failure mode in genetics, convergence, or mechanical structure that ultimately results in nearsightedness. We feel it is premature to discuss these theories until we have a clear understanding of the fundamental behavioral characteristic of the normal eye. We will, therefore, examine the design limitation of a normal feedback controlled eye.
We may define two major environments for this system.
If an individual with a hereditary offset of + 1.0 diopters uses his eyes in an open environment for a long time, his focal status will be approximately defined by the equation:
Focus = Offset + Accommodation - Perturbation * EXP(-t/TAU )
Using typical values:
Focus = + 1.0 + (-.5) - 0 * EXP( - t / TAU )
Focus = + .5 Diopters
This individual will have 20/20 vision with a positive focal state (hyperopic) of + 0.5 diopters.
This generalized analysis has been confirmed by measurements made by Dr. Young on adult "hunting" Eskimos. (6)
If this individual maintains his eyes in a confined visual environment, his eyes will show a slow ramp into myopia. After two or three hundred days his focal status will be:
Focus = +1.0 + (-1.5) - (0) * EXP ( - t / TAU ) Focus = - 0.5 diopters
The same individual, who had 20/20 vision in a normal visual environment, now has 20/40 vision with a focal status of - 0.5 diopters.
A prolonged confined environment violates a design constraint of the human and primate eye. We will define nearsightedness that develops in this way as servo-myopia. This is entirely normal behavior for a normal eye.
This analysis suggests that the normal eye will avoid servoing into nearsightedness if the eye is maintained in an "open" visual environment. Obviously this goal conflicts with the requirement that we spend prolonged hours at close work for the ten to twenty years that we spend in school.
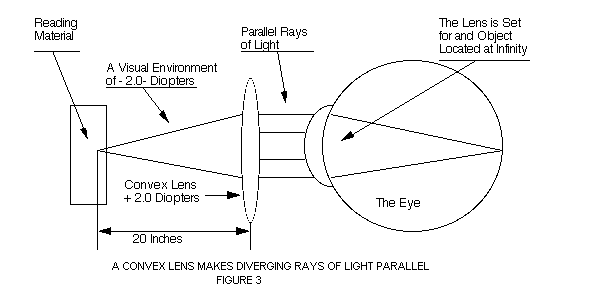
The effect of a confined environment can be neutralized by the use of a convex (plus) lens. A convex lens is a converging lens. Parallel rays of light (from infinity) are brought to a point by this lens.
The converse relationship is true. Diverging rays of light from a nearby object will be made parallel by the use of a convex lens. If reading is done at the focal point of the lens, the value of accommodation will be 0 diopters, rather than -2.0 diopters without the lens. (Figure 3)
As we enter higher academic institutions, our visual environment gradually shifts to a more negative value. We can characterize this increased "near" environment by the following ramp function. (Figure 4)
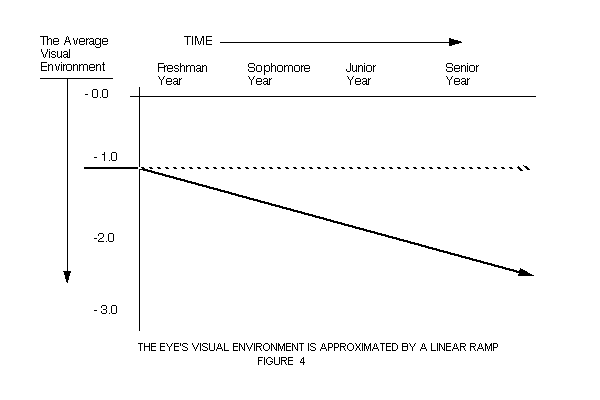
A = m t + b
Where:A = Accommodation (daily average value) from the start of the freshman year.
m = - .001 diopters / day (Estimated)
t = time in days
b = - 1.0 diopters
The Laplace transform of a unit ramp is:
1 / s2
Applying this ramp to the eye's transfer function produces:
System's
Response = [ m / s ^2 ] * [ 1 / ( TAU s + 1 ) ]
The eye's time domain response to a ramp function is:
| Focus (Ramp) | = Offset + Accommodation (Initial Value)
+ Accommodation * TAU [( t / TAU) - 1 + EXP(- t / TAU )] |
After two hundred days, this equation predicts that the eye will show the same linear slope as the accommodation ramp. We can logically expect that the eyes of college students will show a gradual movement towards, and eventually, into myopia when a linear ramp is applied to their accommodation system.
How close does this scenario match the actual situation? In a study of the cadets at West Point, Dr. Gmelin determined that freshmen with 20/20 vision and 0 diopters focal state would, after four years, develop 20/80 vision with -1.3 diopters of myopia. (7) A similar study was conducted at the United States Naval Academy by Dr. Hayden. This study showed an approximately linear change in focal status towards myopia in the eyes of almost all the normal eyed midshipmen. (8)
We have plotted the historical development of myopia as a function of time. (Figure 5) The dynamic theory explicitly states that the eyes of the midshipmen move into nearsightedness due to their increasingly confined visual environment. Their focal status change is in the right direction and proper magnitude to suggest quantitative verification for this dynamic model of the normal eye's long-term behavior.
If their myopia is a result of normal servoing action, a major means of changing this situation would be to use a convex lens for all close work. Use of this lens would substantially alter their visual environment from an estimated value of -1.5 diopters, to a more reasonable figure of -0.4 diopters.
The graph shows the eye's predicted accommodation status as a result of the use of a plus lens. Their resulting focal status was calculated by the use of the equation developed in the previous chapters.
It is difficult to estimate the exact value for the normal eye's time-constant. Dr. Young's work with pigtail macaque monkeys has shown that their eyes have a time-constant of 100 days. Pigtail monkeys weigh 16-28 pounds and grow to maturity in 4-6 years. Since the human is both heavier and matures at a much slower rate, we can expect that the time-constant of the adolescent human eye will be considerably slower. On a preliminary basis we estimate that the specific value is from 100 to 200 days.
Work done during the past twenty years has demonstrated that the accommodation system is a superb example of a physiological control system. It is a complex, sophisticated, and accurate system. We can logically expect that the normal eye will show equal competence in the design of its long-term control system.
The process of building a mathematical model of a physiological system necessarily implies the idealization of that system. Models are not tested in a vacuum. The development of a Helmholtz-dynamic model suggests an opposite model which we will call a Helmholtz-passive theory of the normal eye's behavior.
Heredity is a fundamental constant in both of these theories. There is disagreement on how this factor establishes the eye's long-term focus.
Figure 5 THE EYE'S DYNAMIC RESPONSE TO A CONVEX LENS
ACCOM LONG- HISTO- A = ACCOMMODATION
MODA TERM RICAL F = CALCULATED FOCAL DATA
TION FOCUS FOCUS H = HISTORICAL DATA
DAYS DIOP DIOP DIOP -1.0 -.5 0.0 +.5
TERS TERS TERS ........................................
-84 -1.10 .10 .28 A . F H
-70 -1.10 .09 .27 A . F H
-56 -1.15 .08 .26 A . F H
-42 -1.15 .07 .24 A .F H
-28 -1.20 .06 .23 A .F H
-14 -1.20 .05 .21 A .F H
0 -.40 .04 .20 >>------------->A .F H
14 -.40 .06 .19 Step Input A .F H
28 -.40 .09 .17 (Plus Lens Use) A . FH
42 -.40 .11 .16 A . FH
56 -.40 .13 .14 A . H
70 -.40 .16 .13 A . H
84 -.40 .18 .12 A . H F Helmholtz
98 -.40 .20 .10 The Average A . H F Dynamic
112 -.40 .22 .09 Value of A . H F Response
126 -.40 .23 .07 Accommodation A .H F <------<<
140 -.40 .25 .06 >>------------> A .H F
154 -.40 .27 .05 A .H F
168 -.40 .28 .03 A .H F
182 -.40 .30 .02 A H F
196 -.40 .31 .00 A H F
210 -.40 .33 -.01 A H F
224 -.40 .34 -.02 A H F
238 -.40 .35 -.04 A H. F
252 -.40 .36 -.05 A H. F
266 -.40 .37 -.07 Helmholtz Passive A H. F
280 -.40 .38 -.08 Predicted Response A H . F
294 -.40 .39 -.09 >>----------------------> H . F
308 -.40 .40 -.11 A H . F
322 -.40 .41 -.12 A H . F
336 -.40 .42 -.14 A H . F
350 -.40 .43 -.15 A H . F
364 -.40 .44 -.16 A H . F
378 -.40 .45 -.18 A H . F
392 -.40 .45 -.19 A H . F
406 -.40 .46 -.21 A H . F
420 -.40 .47 -.22 A H . F
434 -.40 .47 -.23 A H . F
.........................................
-1.5 -1.0 -.5 0.0 +.5
DIOPTERS: NEGATIVE POSITIVE
Actual myopia prevention is a very difficult task to accomplish; however, we have been able to demonstrate that effective myopia prevention is a reasonable expectation, provided the convex lens is assiduously and intelligently used for all close work.
The belief that this approach will work is reflected in current eye care practices. About twenty percent of the profession will use the plus lens (bifocal) to deal with the problem of incipient myopia. The experimental data shows two facts:
If one is willing to make the scientific and physical commitments necessary to be part of a nearsightedness avoidance effort, there is a high probability the effort will be completely successful.
1. Campbell, F. W., Robinson, J.G. DYNAMICS OF ACCOMMODATION RESPONSES OF THE HUMAN EYE. J. Physiol., 151:258-295 London 1960
2. Brown, O. Young, F. THE RESPONSE OF A SERVO CONTROLLED EYE TO FOCAL PERTURBATIONS, The 2nd Annual Conference of the IEEE EMBS pp. 6.7.1 - 6.7.4 1980
3. Brown, O. Young, F. Berger, R. MEASURING THE EYE'S FOCAL ACCURACY: A HEURISTIC APPROACH, The 3rd Annual Conference of the IEEE EMBS 1981
4. Brown, O. Young, F. THE RESPONSE OF A SERVO CONTROLLED EYE TO A CONFINED VISUAL ENVIRONMENT, The 18th Annual Rocky Mountain Bioengineering Symposium pp. 41-44 1981
5. Brown O., Berger R., A NEARSIGHTEDNESS COMPUTER, Proceedings of the Annual New England bioengineering Conference pp. 343-346 1979
6. Young, F. THE TRANSMISSION OF REFRACTIVE ERRORS WITHIN ESKIMO FAMILIES, American. J. Optometry. and Arch. Am. Acad. Optometry., 49(9): 676-685, 1969
7. Gmelin, R. T. MYOPIA AT WEST POINT: PAST AND PRESENT, Military Medicine 141(8) 542-3 Aug. 1976
8. Hayden, R. DEVELOPMENT AND PREVENTION OF MYOPIA AT THE UNITED STATES NAVAL ACADEMY, Archives of Ophthalmology, Volume 25, #4 April 1941