

| How To Avoid Nearsightedness
|
The task of science is both to extend the range of our experience and to reduce it to order, and this task presents various aspects inseparably connected with one another. Only by experience itself do we come to recognize those laws that grant us a comprehensive view of the diversity of phenomena. As our knowledge becomes wider, we must even be prepared therefore, to expect alterations in our point-of-view that are best suited for the ordering of experience. - Niels Bohr
The normal human and primate eye maintain long-term focal accuracy in the presence of focal perturbations. It is difficult to measure the magnitude of the perturbations and the effectiveness of the consequent dynamic response. By making reasonable assumptions based on a physiological model, we can obtain a more accurate numerical value for the eye's focal accuracy.
Previous experiments have demonstrated that the normal eye sets its long-term focus by a dynamic process. (1) The time response of the eye to a focal perturbation in the eye's optical system is given by: (2)
While the equation can account for the eye's response, it cannot yield a direct measure of the eye's focal accuracy. As previously established, the eye must overcome continuous micro-perturbations while growing to maintain accurate focus. What experimental technique can we employ to measure the magnitude of the perturbations in the eye's focal positioning mechanism?
There is experimental evidence which suggests that each eye sets its long-term focus independently of the other eye. (3) Making use of this evidence we may model the left and right eye as two independently tracking mechanisms.
Each eye uses its own accommodation signal to drive the long-term focal setting system. (4) Short-term, the eyes are cross-linked in vergence and accommodation. (5) In this model, each eye has irreducible noise in the actuator, which appears as perturbations in the focal status of the eye. (See Figure 1)
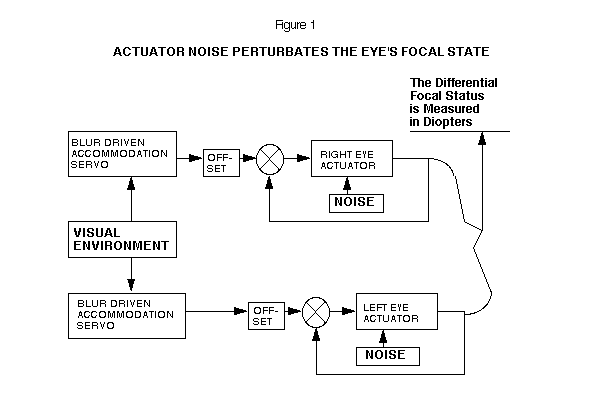
The function, 1/(TAU s + 1), for the eye's behavior has a time-constant of 100 days. The offset of the normal eye has a value of +1.5 diopters. A Bode graph of this transfer function is shown on Figure 2. The high frequency components of noise will be attenuated, and the eye's focal status will change very slowly on a day-to-day basis.
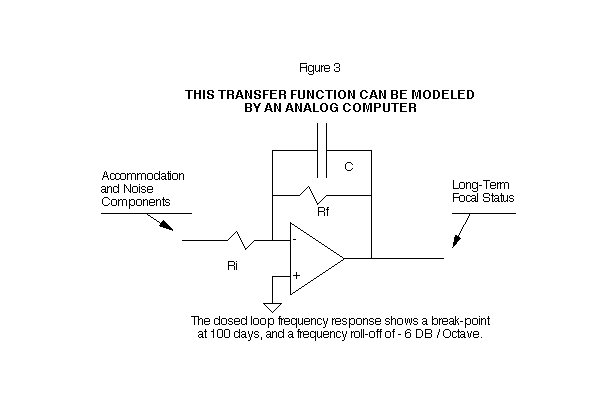
The closed loop frequency response shows a break point at 100 days, and a frequency roll-off of -6 DB/Octave. This transfer function can be modeled by an analog computer. (See Figures 2 and 3)

It is difficult to completely measure the average visual environment on a day-to-day, month-by-month basis. We cannot directly measure the amount by which the eye's focus is perturbated away from its commanded (visual environment) position, if we cannot accurately measure the visual environment. We must find an alternative approach to check the eye's tracking accuracy which will obviate the need for a precisely measured environment.
Three reasonable assumptions that must be made in order to obtain a statistical specification of the eye's RMS (Root Mean Square) focal noise are:
If the eye's control system were perfect, you would find the focal setting of the left eye identical to the right. The extent to which this is not the case will give us a means to determine the eye's tracking accuracy.
Because we cannot control the eye's average visual environment, we cannot easily measure the perturbations that occur in each eye. We can, however, measure the differential focal status developed between the left and right eye. This technique is based on the statistical principle that the squares of noise sources may be added algebraically. (6)
The same factors that produce perturbations in the left and right eye are equivalent for both eyes, assuming the underlying noise process is ergodic, which is highly probable for all normal eyes. We, therefore, combine the noise in the left and the right eye:
Using the equation in this form will allow us to measure the differential focal status of one individual over a period of months. This sequence of measurements will give us a continuing accounting of the eye's tracking accuracy, even though the average visual environment is changing. Measurement of noise by this technique is called a time-series measurement of a stationary random process.
In order to demonstrate how the changing focal status of the left and right eye generates a third (differential) noise statistic, we programmed a FORTRAN random number generator to simulate the noise in the left and right eye. The program then calculates the differential measurement by subtracting the left eye's focal status from the right eye's focal status. The three noise measurements are plotted on a weekly basis. (See Figure 4)
Differential2 = Left2 + Right2
( .213)2 = ( .151)2 + ( .151)2
The individual noise values in the program that actually produced the differential noise statistic are:
Left = 0.124 diopters Right = 0.174 diopters
The average of these two numbers is 0.149 diopters RMS. Our estimate, calculated from the differential value, is .151 diopters RMS.
"In dealing with stationary random processes, it is usually assumed that Time Averages are equivalent to Ensemble Averages. This is the so-called ergodic hypothesis of statistical mechanics." (7)
Dr. Berger carried out the required ensemble differential measurement during the course of his normal eye examinations. Because we are interested in the noise level in the normal eye, patients with normal vision were chosen for the statistical sample.
Figure 4: A CONCEPTUAL NOISE MODEL FOR THE LEFT AND RIGHT EYE
(USE CORRECTED GRAPH, SEE FIRST EDITION OF THIS BOOK)
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
FOCAL STATUS: LEFT EYE X RIGHT EYE
LEFT RIGHT DIFF. DIOPTERS X DIOPTERS
TIME EYE EYE (R-L) +.5 +1 X .0 +.5
WEEK DIOP. DIOP. DIOP .........................X......................
1 .50 .50 .00 L R
2 .34 .47 .13 L . R.
3 .42 .40 -.02 L . R .
4 .50 .25 -.25 L R .
5 .35 .21 -.14 L . R .
6 .38 .12 -.26 L . R .
7 .47 .12 -.34 L. R .
8 .34 .12 -.22 L . R .
9 .31 .37 .06 L . R .
10 .59 .41 -.17 . L R .
11 .44 .43 -.01 L. R.
12 .65 .45 -.20 . L R.
13 .64 .49 -.15 . L R
14 .55 .41 -.14 .L R .
15 .45 .16 -.29 L. R .
16 .48 .16 -.32 L R .
17 .37 .11 -.26 L . R .
18 .52 .19 -.33 L R .
19 .58 .11 -.47 . L R .
20 .54 .29 -.26 .L R .
21 .70 .42 -.28 . L R .
22 .64 .31 -.34 . L R .
23 .67 .35 -.32 . L R .
24 .69 .19 -.49 . L R .
25 .67 .32 -.35 . L R .
26 .61 .28 -.33 . L R .
27 .64 .42 -.22 . L R .
28 .43 .20 -.23 L. R .
29 .36 .59 .23 L . . R
30 .49 .59 .10 L . R
31 .57 .70 .14 .L . R
32 .49 .70 .21 L . R
33 .64 .69 .04 . L . R
34 .69 .61 -.08 . L . R
35 .61 .40 -.21 . L R .
36 .55 .18 -.37 .L R .
37 .65 .20 -.45 . L R .
38 .65 .16 -.49 . L R .
39 .70 .09 -.61 . L R .
.................................................
SUMMARY OF RMS RESULTS FROM THE ABOVE GRAPH
LEFT = .124 DIOPTERS RIGHT = .174 DIOPT. DIFF. = .211 DIOPT.
NOISE` RMS NOISE RMS NOISE RMS
(NOT PLOTTED)
The following focal states (Table 1, below) shows the focal status of individuals, selected at random, from the age of 5 to 25. The RMS value is calculated from the differential measurement.
TABLE 1: THE DIFFERENTIAL FOCAL STATUS OF INDIVIDUALS SELECTED AT RANDOM ID OD AGE RIGHT LEFT DIFFERENCE 1. SJ RB 14 .75 .50 .25 2. JB RB 19 .50 .12 .38 3. RM RB 20 .50 .50 .00 4. AS RB 11 .00 .00 .00 5. MA RB 16 .62 .75 -.13 6. ST RB 22 .12 .12 .00 7. BT RB 12 1.25 1.12 .13 8. RV RB 16 .00 .25 -.25 9. MT RB 18 .25 .62 -.37 10. YM RB 13 1.00 1.00 .00 11. SV RB 19 .50 .50 .00 12. TH RB 17 .75 .50 .25 13. CR RB 20 .25 .25 .00 14. NC RB 12 1.25 1.50 -.25 15. BS RB 14 .62 .62 .00 16. SH RB 13 .25 .62 -.37 17. HR RB 15 .75 .75 .00 18. RC RB 20 .50 .13 .37 19. DD RB 18 .25 .50 -.25 20. FR RB 23 .50 .62 -.12 DIFFERENTIAL FOCAL STATE = 0.213 DIOPTERS RMS
The ensemble differential measurement for this group of individuals is 0.213 diopters RMS. The differential equation allows the calculation of the a noise level in each individual eye of:
DIFFERENTIAL * .707 = INDIVIDUAL EYE NOISE
(.213) * .707 = .151 Diopters RMS
EYE NOISE * .674 = PROBABLE ERROR
(.151) * .674 = 0.10 DIOPTERS
In a positioning servo, we would predict that the actual position would be within 0.1 diopters of the command position 50 percent of the time. The eye is about 2.44 cm in length and must have a focal power of 57 diopters in order to focus light on the retina. In terms of percent, the eye has a tracking probable error of: 0.10/57 = 0.17 percent.
The eye tracks its environment with a probable error of 0.1 diopters. What are the experimental implications of a control system with this degree of accuracy?
Previous experiments lead us to believe that the normal eye sets its long-term focus by a dynamic process. Physiological systems are complex and contain parameters which are not always clearly defined nor easily measured. We, therefore, have had to make assumptions and simplification in order to make the long-term behavior of the normal eye intelligible to ourselves and others.
There are major experimental difficulties involved in attempting to directly measure the accuracy with which the normal eye tracks its visual environment. A physiological model of the eye's behavior implies a certain level of tracking accuracy. By making use of the fact that each eye tracks the same visual environment we may, by an indirect approach, determine the eye's focal accuracy.
This chapter requires insight into the fundamental behavior of an optical system in the presence of perturbations. Further, a knowledge of statistics is required. By using these specialized but essential analytic techniques it is possible to establish the basic tracking accuracy of the normal eye. This would be very difficult to do by direct experimentation.
We believe that the eye is sophisticated in its design and must employ feedback (dynamic) control principles to overcome the inevitable perturbations that occur to it as it grows. Only in this way can the eye achieve a high order of focal precision.
1. Brown, O., Young, F., THE RESPONSE OF A SERVO CONTROLLED EYE TO A CONFINED VISUAL ENVIRONMENT, The 18th Annual Rocky Mountain Bioengineering Symposium, Laramie, Wyoming (4/81)
2. Brown, O., Young, F., THE RESPONSE OF A SERVO CONTROLLED EYE TO FOCAL PERTURBATIONS, The 2nd Annual Conference of the IEEE Engineering in Medicine and Biology Society (9/80)
3. Bedrossian, R.H., THE EFFECT OF ATROPINE ON MYOPIA, Annals of Ophthalmology, 3 (8): 890-899 (In this study of myopia development, accommodation in one eye was prevented with atropine while the other was not. Result: The atropinized eye stabilized, while the non-atropinized eye progressed into myopia.)
4. Stark, L. NEUROLOGICAL CONTROL SYSTEMS Section III, Plenum Press, New York (1966)
5. Hung, H.K., Semmlow, J.L., STATIC BEHAVIOR OF ACCOMMODATION AND VERGENCE: COMPUTER SIMULATION OF AN INTERACTIVE DUAL-FEEDBACK SYSTEM. IEEE Transactions on Bioengineering, volume BME-27, #8, pp 439-447 (8/80)
6. Schwartz, M., INFORMATION TRANSMISSION, MODULATION AND NOISE, pp 216, McGraw-Hill (1959)
7. Phillips, R.S., Nichols, N.B., Hubert, J.M., THEORY OF SERVOMECHANISMS, pp 217, McGraw-Hill (1947)
8. Young, F., THE EFFECT OF RESTRICTED VISUAL SPACE ON THE PRIMATE EYE. American Journal of Ophthalmology, Volume 52, N.5, Part II ( 11/61)